
Part of X-Team's culture is about being Unleashed to pursue your interests, passions, and hobbies all while leveling-up professionally.
Today we're going to combine three sweet topics that are personal favorites of mine into one (hopefully) interesting article:
- Philosophy
- Gaming
- Computer Science
Are these three topics really as disparate as they might at first appear? I argue no and I hope to show you by article's end that all three weave together into some ultra-cool practical magic!
We're going to take a quick trip across mathland and learn how some cool people pretty much invented Procedural Generation back in the 1600's. Oh yeah!
Modal Logics and Possible Worlds Semantics
Way back when, there was this super rad dude named Leibniz (yeah that Leibniz ...Gottfried I Mother Fk'in Invented Calculus then Predicted the Computer Leibniz ... Gottfried Who The Hell Is This Descartes Guy Leibniz) who pretty much predicted the Universal Turing Machine and Modern Symbolic Mathematics (with his Calculus Ratiocinator or Characteristica Universalis).
Dude also figured out a lot about what we call Modal Logic today (work within which has resulted in numerous Rolf Shock awards which are basically the equivalent of the Wolf Prize or the Nobel Prize for philosophy - I've had the honor of working with several winners and have to agree that they are pretty badass)!
For those who dug learning about Boolean Algebra (Classical Logic from an Algebraic perspective), you might enjoy learning more about Modal Logic. Here, for example, are the S5 Modal Logic Axioms which define notions like necessity (□) and possibility (◊):
[D] □A → ◊A
[T] □A → A
[B] A → □◊A
[S4] □A → □□A
[S5] ◊A → □◊A
As a result, we can frame a lot of our chat about possibility talk (modality) and procedurally generated worlds (like those found in video games) using Modal Logic and, more specifically, Kripke semantics for Modal Logic!
Check out these sweet visuals diagramming the relationship between different Modal Axiom Systems:
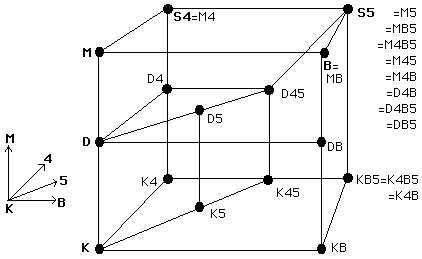
(Source: SEP)
What's relevant to us here is the idea of possible worlds which are formally defined thusly:
[1] A set <W, R, V> is a Kripke Model for L2 just in case:
[A] [i] W ≠ ∅
[ii] R ⊆ W х W
[iii] V : A х W → {⊥, ⊤}
[B] [i] Each w ∈ W is called a possible world
[ii] For each p ∈ A: p ∈ wff(L2)
[2] Truth of a modal formula p at a possible world w in a
relational structure M = <W, R, V> is denoted 'M,w ⊨ p'
and is inductively defined as follows:
[A] M,w ⊨ p just in case V(p, w) = ⊤
[B] M,w ⊨ ⊤ and M,w ⊭ ⊥
[C] M,w ⊨ ¬p just in case M,w ⊭ p
[D] M,w ⊨ p & q just in case M,w ⊨ p & M,w ⊨ q
[E] M,w ⊨ □p just in case (∀ v ∈ W)(wRv → M,v ⊨ p) [F] M,w ⊨ ◊p just in case (∃ v ∈ W)(wRv & M,v ⊨ p) And we can visualize a frame specified by the above constraints here:
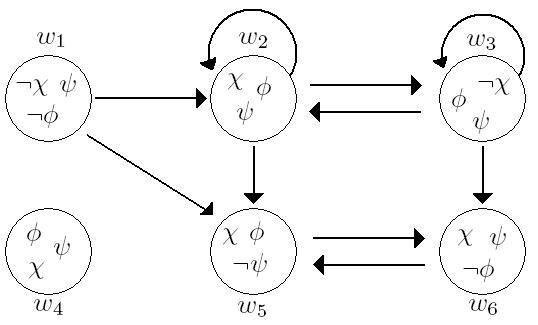
(Source: Wikimedia Commons)
In other words, given a Kripke Model we get a bunch of worlds such that certain propositions are true at them and others false. Every world is slightly different and we can order worlds by how similar they are, whether they can be epistemically accessible from each other, and define either total or partial truth-functions that more or less define all variations of difference between them.
These seemingly esoteric, academic, and blue-skies math topics have actually found a place in many more familiar and practical areas including formal semantics (Natural Language Processing, linguistics), computer science, and game development!
State of Affairs and Game State
One of the concepts derived from nascent philosophical investigations about the nature of reality and truth that persists in Computer Science is the idea of state (as in application state) which originated in discussions surrounding states of affairs (sets of facts, propositions, or possible worlds).
For those familiar with the gaming industry, several big name titles have launched heralding a new age of procedurally generated content:

(Image Source: GOG)
No Man's Sky provides over 18 quintillion worlds that are dynamically generated from seed data specifying unique characteristics for each world rather than maintaining static content for each and every one of those worlds!


(Image Sources: Humble Bundle)
In fact, this approach was predicted by the legendary computer scientist Jurgen Schmidhuber who argued that the fastest way to build a world/universe is to create an algorithm that builds every possible world/universe!
Procedural Generation Basics
Procedural Generation involves creating some content according to a fixed set of rules. Usually, this implies generating a LOT of content (like the 18 quintillion worlds of No Man's Sky). Below, we'll keep things a little simpler!
We need to create a way of storing unique objects - we can think of this as the DNA for a specific copy of whatever we're trying to procedurally produce (indeed, one branch of procedural generation is the study of genetic or eveolutionary algorithms):
/** * Generate Seed. * * @param - arr - [4, 2, 3] - generates a seed of length 3 such * that each char is bounded by the corresponding arr index. */
var create = function (arr) {
var seed = ""
for (var i = 0; i < arr.length; i++) {
seed += Math.floor(Math.random() * arr[i]);
}
return seed;
}
This seed will express a unique object when it's parsed dynamically:
/** * Potion Mapping. */
var mappings = [
'#9C27B0',
'#673AB7',
'#2196F3',
'#FF9800',
'#D32F2F'
]
/** * Potion. * @param - seed - e.g. 12, 11, 44 */
var Potion = function (seed) {
var color_top = parseInt(seed.charAt(0))
var color_bottom = parseInt(seed.charAt(1))
get('potion', 1, 4).style.backgroundColor = 'black'
get('potion', 1, 5).style.backgroundColor = 'black'
get('potion', 2, 3).style.backgroundColor = 'black'
get('potion', 2, 4).style.backgroundColor = mappings[color_top]
get('potion', 2, 5).style.backgroundColor = mappings[color_top]
//...
}
Potion(create([4,4]));
}
We see that each information unit of our seed string is finitely bound. Above, there are at most 25 combinations. We observe that the delimiting cases are invariance (no change at all) and total change (randomly showing entirely different images).
Simple Variation Alchemy
Using our simple example above, we can procedurally generate potions! We're not getting too carried away here since we'll be reusing the same template (shape, size) for each potion bottle. We could, however, enrich the example with alternative bottle and cork types. For now, our simple example will suffice.
A first example made from 23:
A second example made from the seed 42:
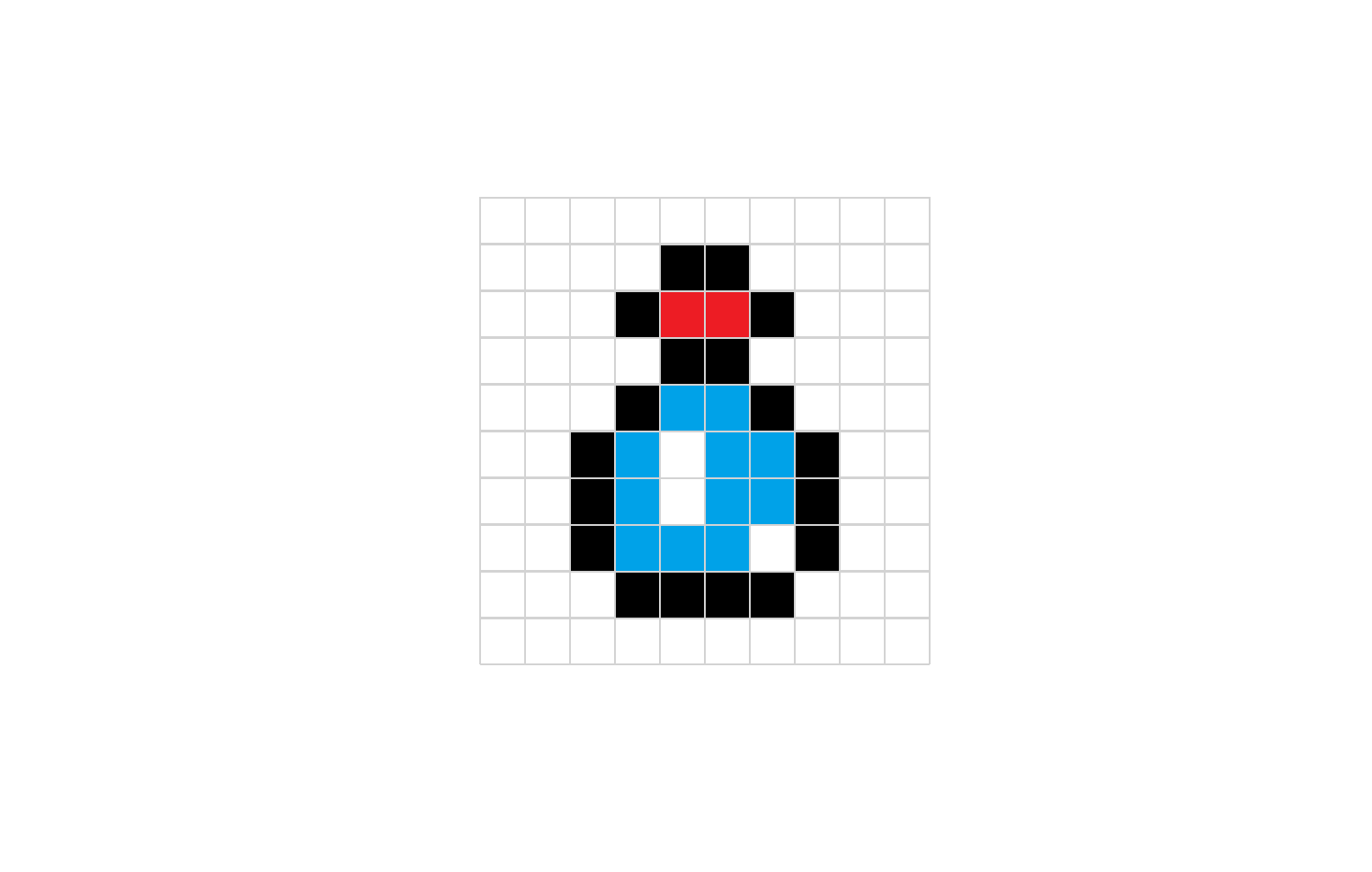
Pretty sweet, right? If we let our creativity run wild, we can imagine all kinds of components, colors, styles, parts, and so on that can be combined in new but controlled ways!
Building a World
The next example combines a few insights form the previous one but with a slightly more ambitious aim - instead of a generating alternating colors of a potion bottle, let's create a reasonable game board by procedurally generating roads.
We'll have grass squares:

And we'll have road squares:

/** * Automata mapping. */
var mappings = [
'/image/grass.jpg',
'/image/road.jpg'
]
Every road square that's placed should have another road square placed directly to it's right if such a space exists!
/** * Road function. */
var road = function (s, r, c) {
if (c > 0 && get('tiles', r, c - 1)
.style
.backgroundImage === "url(\"" + mappings[1] + "\")") return mappings[1]
if (r > 0 && get('tiles', r - 1, c)
.style
.backgroundImage === "url(\"" + mappings[1] + "\")") return mappings[0]
return mappings[parseInt(s.charAt((r * 5) + c))]
}

Tiles(create([2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]))
We've applied a very simple algorithm to create a simple gameworld backdrop from a randomly generated seed. The possibility space (or the collection of every possible permutation of tile arrangments) is finite, so we can reason about how many variations we need and how they should behave.
/** * Tiles. * * @param seed - e.g. 01010 00000 00000 00000 00000 */
var Tiles = function (seed) {
for (var i = 0, j = 0; i < 5 && j < 5;) {
get('tiles', i, j).style.backgroundImage = 'url(' + road(seed, i, j) + ')'
j++
if (j === 5) {
i++
j = 0
}
}
}
The example we've made above clearly doesn't approach the scale and level of awesome that No Man's Sky does, but the idea we've employed above does help to illustrate some of the underlying mechanics at play.
Rechendur Raum, The Game of Life, and Cellular Automata
Expanding on our simple procedurally generated world example above, let's liven up our world with some activity. The famous computer scientists Konrad Zuse wrote in Rechendur Raum that our physical universe is really some kind of quantum computer.
Later theorists like the great entrepreneur Stephan Wolfram have argued that computer and information science is actually more fundamental than physics. Either way, there's a lot of fun we can have with this line of thinking.
Conway's Game of Life
Conway's Game of Life was one of the first attempts to model ecological and biological systems using software. Moreover, the fundamental precept is that such systems are actually controlled by finite rules that are uniformly applied over time.
The original Game of Life was defined by the following rules (and can be seen here):
[UNDERPOP] Any live cell with fewer than two live neighbors dies.
[SUSTAIN] Any live cell with two or three live neighbors lives.
[OVERPOP] Any live cell with more than three live neighbors dies.
[REPRO] Any dead cell with exactly three live neighbors becomes a live cell.
Let's create our own using the same tile pieces from before but this time adding two new critters:
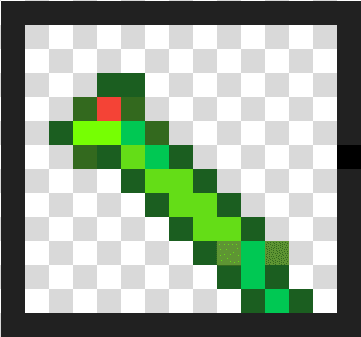

Our rules will be:
[BOOSNAKE] A snake removes all adjacent cats.
[FURBABY] Two adjacent cats create a third cat.
[RANDOM] Snakes randomly move, slight randomization.
We thus derive across about 15 cycles the following three world states:
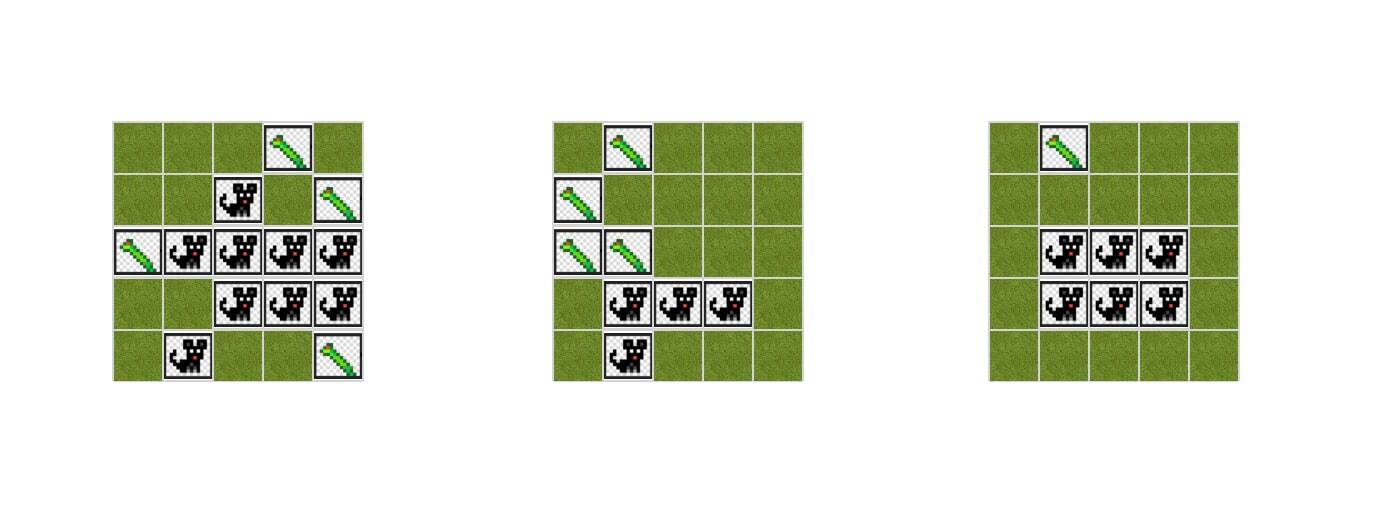
Fun to combine possible worlds with temporal evolution! We might even imagine that our universe is some giant simulation! Wow!
For some way more awesome examples, check out:
- Platane's Procedural Flower for JavaScript!
- The SpaceshipGenerator in Python!
- An OpenGL 3DWorld!
Conclusion
Thanks for joining me for a concise introductory walk-through covering some basic procedural generation, philosophy, and computer science topics!
If you'd like to tinker around with the code yourself, check out GitHub!
Shout Out's
- Great free tile assets from OpenGameArt.org!
- PixelArt.com!
TABLE OF CONTENTS



