Meet Steve. He's a shy, withdrawn American who's helpful when asked, but otherwise not interested in people. Steve likes detail, order, and putting things in the right places. Is he a farmer or a librarian?
As the psychologists Amos Tversky and Daniel Kahneman showed in their paper Judgment under Uncertainty, most people guess that Steve is a librarian. But he's probably not. He's almost certainly a farmer. Sounds counter-intuitive? It's not. It's Bayes' theorem at work.
This article will explain what Bayes' theorem is (including why Steve is a farmer) and how you can use it to lead a more rational life where you make smarter decisions and fewer mistakes.
What is Bayes' Theorem?
Bayes' theorem is a formula for calculating conditional probabilities. In plain words, it's a way to figure out how likely something is under certain conditions. Let's explain the theorem with an intuitive example first and a mathematical example next.
Example 1: The Problem with Medical Tests

You're at the doctor's office for a routine checkup. She tests you for a rare disease that occurs in 0.1% of the population. The disease has debilitating effects and is impossible to cure.
You test positive.
The test correctly identifies 99% of the people who have the disease. It incorrectly identifies 1% of the people as having the disease even though they don't—the so-called false positives.
If the test is 99% accurate, does this mean there's a 99% chance you have the disease when you test positive? It doesn't. The chances that you have the disease are much lower. To understand why, let's flip around the scenario.
Consider 1,000 randomly sampled people in a big room. One person in the room will have the disease, because its prevalence is 0.1%. However, because the test has a false positive rate of 1%, ten people will test positive even though they don't have the disease.
So there will be eleven people who test positive, but only one will have the disease. That's why, once you've tested positive, your chances of having the disease aren't 99%. They're one in eleven, or 9%.
Example 2: Let's Talk About Steve

Most people think Steve is a librarian because of his description. He's shy, withdrawn, likes order, etc. All characteristics that seem to fit a librarian. We place so much emphasis on his description that we forget to incorporate information about the total number of farmers versus librarians.
According to the American Library Association, there are 166,194 librarians in the United States today. Meanwhile, according to the US Department of Agriculture, there are at least 2.6 million farmers. So the ratio is approximately one librarian for every fifteen farmers.
For the sake of explaining Bayes' theorem, let's assume that Steve's description fits around 70% of all librarians and 30% of all farmers. We now have enough information to dig into Bayes' formula.
We're looking for the Probability that Steve is a Librarian given the Description. In the formula, we write this down as P(L|D). All the other parts of the formula are:
P(L)= the probability that Steve is a librarian, 1/15 or 0.067.P(F)= the probability that Steve is a farmer, 0.933.P(D|L)= the probability that the description fits a librarian, 0.7.P(D|F)= the probability that the description fits a farmer, 0.3.
Let's now build Bayes' formula. For the numerator, we need to multiply the probability that the description fits a librarian, P(D|L), with the probability that Steve is a librarian before we'd read his description, P(L).
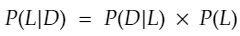
Next, we need to divide the numerator with the probability that Steve is a librarian, P(L), times the probability that the description fits a librarian, P(D|L), plus the probability that Steve is a farmer, P(F), times the probability that the description fits a farmer, P(D|F).
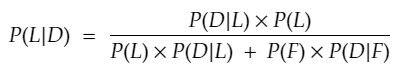
Time to plug in the numbers:
P(L|D) = (0.7 x 0.067) / (0.067 x 0.7 + 0.933 x 0.3)
P(L|D) = 0.0469 / (0.0469 + 0.2799)
P(L|D) = 0.0469 / 0.3268
P(L|D) = 0.14There you have it. The chances that Steve is a librarian are only 14%.
This is what makes Bayes' theorem so powerful. It allows you to quantify probabilities, which is why it's heavily used in medicine, statistics, machine learning, risk analysis, and other math-heavy fields full of probabilities.
But it's also a powerful tool to think more rationally as an individual.
How to Apply Bayesian Thinking to Your Life
The point of this article isn't for you to memorize Bayes' formula and calculate probabilities wherever you go. That's entirely impractical. The power of Bayes' theorem for the individual lies in the three implicit lessons that come with it. Let's go over each one.
Be Careful with New Evidence
Had you been asked if Steve were a librarian or a farmer before you'd read his description, what would you have said? You wouldn't have known anything about Steve, so you might have said he could be either of the two jobs. You might even have considered the ratio between farmers and librarians, and said he was probably a farmer.
But when you're given a small piece of evidence, Steve immediately becomes a librarian. All of us are guilty of placing far too much emphasis on new evidence, to the point where we sometimes flip-flop between opinions because of evidence and counter-evidence. For example:
- UFOs didn't exist until the Pentagon UFO report and now it's beyond a shadow of a doubt that UFOs exist.
- Nuclear power was a great way to generate clean energy until the Fukushima Daiichi accident and now we must shut down all nuclear plants.
This isn't rational thinking, because it's too volatile, too fast. Bayes' theorem is a reminder to update our beliefs incrementally, according to the strength of the evidence. If the evidence isn't empirically convincing and consistently replicable, don't take it at face value. Instead, evaluate carefully and move your beliefs appropriately.
Accept Other Opinions
Bayes' theorem explains why two people might see the same evidence and come up with entirely different conclusions. They simply have different priors. A prior, or prior probability, is what you believed before you encountered new evidence. In our example with Steve, that was the probability that he was a librarian before we'd read his description, P(L).
When you're talking about beliefs, priors aren't easily quantifiable. You have to look at them relatively. For example, if you grew up in a neighborhood full of crime, your belief that crime is part of life might be 75% when you compare it to the person who grew up in a neighborhood without any crime, for who it might be 5%.
If you both see a crime, your beliefs that crime is a part of life should increase incrementally, but for you it might move to 80% while for the other it might move to only 10%.
Bayes' theorem makes it easier to understand why people see the world in different ways. It encourages us to empathize with others. They might be thinking rationally; they're just coming at it from different backgrounds.
Prove Yourself Wrong
Bayes' theorem is a tool for thinking rationally, but only if you're willing to search for evidence that proves you wrong. Do not ignore such evidence and do not disregard it without proper diligence. Instead, seek it out.
If you don't, you'll end up in an alternate reality where your beliefs are constantly proven right despite possibly overwhelming evidence to the contrary. It's the world of conspiracy theories, home to those who are willingly blind to the truth:
- Climate change deniers;
- Anti-vaxxers;
- Flat-Earthers;
- Holocaust deniers.
Finding evidence that proves you wrong is harder than it seems, in large part because the Internet is set up in such a way it often encourages what you already believe without showing you the flip side of the coin.
But it's exactly because it's hard that it's important. You have to search for the evidence you don't like, so your beliefs can inch ever closer to the truth.
In Conclusion
This article has explained that Bayes' theorem is a mathematical way to calculate conditional probabilities. It did so with an intuitive example and a mathematical example.
Next, it spoke about the three ways you can apply Bayesian thinking to your life. Use Bayes' theorem to evaluate new evidence, accept other opinions, and seek evidence that proves you wrong. Do this consistently, and you'll be able to live a life of rational integrity.



